El Fin Del Conocimiento - Bóveda 5/80 - CVPR - 2022 - Aprendizaje de Formas en Imágenes Biomédicas

graph LR classDef shape fill:#f9d4d4, font-weight:bold, font-size:14px classDef learning fill:#d4f9d4, font-weight:bold, font-size:14px classDef manifolds fill:#d4d4f9, font-weight:bold, font-size:14px classDef applications fill:#f9f9d4, font-weight:bold, font-size:14px classDef geomstats fill:#f9d4f9, font-weight:bold, font-size:14px A["Aprendizaje de Formas en
Imágenes Biomédicas"] --> B["Aprendizaje de formas:
aprendizaje automático en formas 1"] A --> C["Imágenes biomédicas:
estructuras biológicas, varias escalas 2"] C --> D["Vínculo forma-biología:
estructura, función, salud 3"] C --> E["Técnicas de imagen:
RMN, microscopía, crio-EM 4"] C --> F["Preguntas biomédicas:
cambios de forma, enfermedad 5"] C --> G["Reconstrucción de formas:
extracción de imágenes 6"] B --> H["Modelado/representación de formas:
representación numérica para análisis 7"] A --> I["Variedades: generalizaciones
curvadas de espacios vectoriales 8"] I --> J["Formas como variedades:
superficie del objeto 9"] I --> K["Espacios de formas como variedades:
todas las formas posibles 10"] I --> L["Espacios de transformación de formas
como variedades: movimientos, deformaciones 11"] B --> M["Estadísticas generalizadas
a variedades 12"] M --> N["Geometría de variedades:
sesgo inductivo para el aprendizaje 13"] B --> O["Problemas de ML en variedades:
supervisado, no supervisado, RL, optimización 14"] O --> P["Bloques de construcción de aprendizaje en variedades:
puntos, tangentes, geodésicas, distancias 15"] O --> Q["Conversión de espacio vectorial a
ML en variedades 16"] A --> R["Geomstats: paquete de Python
para cálculos en variedades 17"] R --> S["Aprendizaje en variedades de Riemann 18"] R --> T["Variedades de posición/transformación: SE3 19"] R --> U["Taxonomía de variedades:
de abstracto a concreto 20"] B --> V["Visión general de ML adaptado a variedades 21"] V --> W["Reducción de dimensión en variedades:
PCA, autoencoders 22"] W --> X["Vista geométrica:
subespacios principales 23"] V --> Y["Autoencoders variacionales VAEs 24"] Y --> Z["Generalizando VAEs a variedades 25"] Z --> AA["Componentes de mVAE:
mapa exponencial, distancia geodésica 26"] Z --> AB["mVAE vs alternativas:
más rápido que MCMC 27"] Z --> AC["mVAE explica
curvatura del espacio latente de VAE 28"] A --> AD["Pipeline de análisis de formas:
extracción, modelado, variedades, ideas 29"] A --> AE["Investigación en curso:
generalizar ML, aplicaciones biomédicas 30"] class A,H,M,N,V,W,X,Y,Z,AA,AB,AC learning class B,D,F,G,J shape class C,E applications class I,K,L,O,P,Q,S,T,U manifolds class R geomstats

Resumen:

1.- Aprendizaje de formas: Aprendizaje automático en datos que son formas, con cada punto de datos siendo una forma.

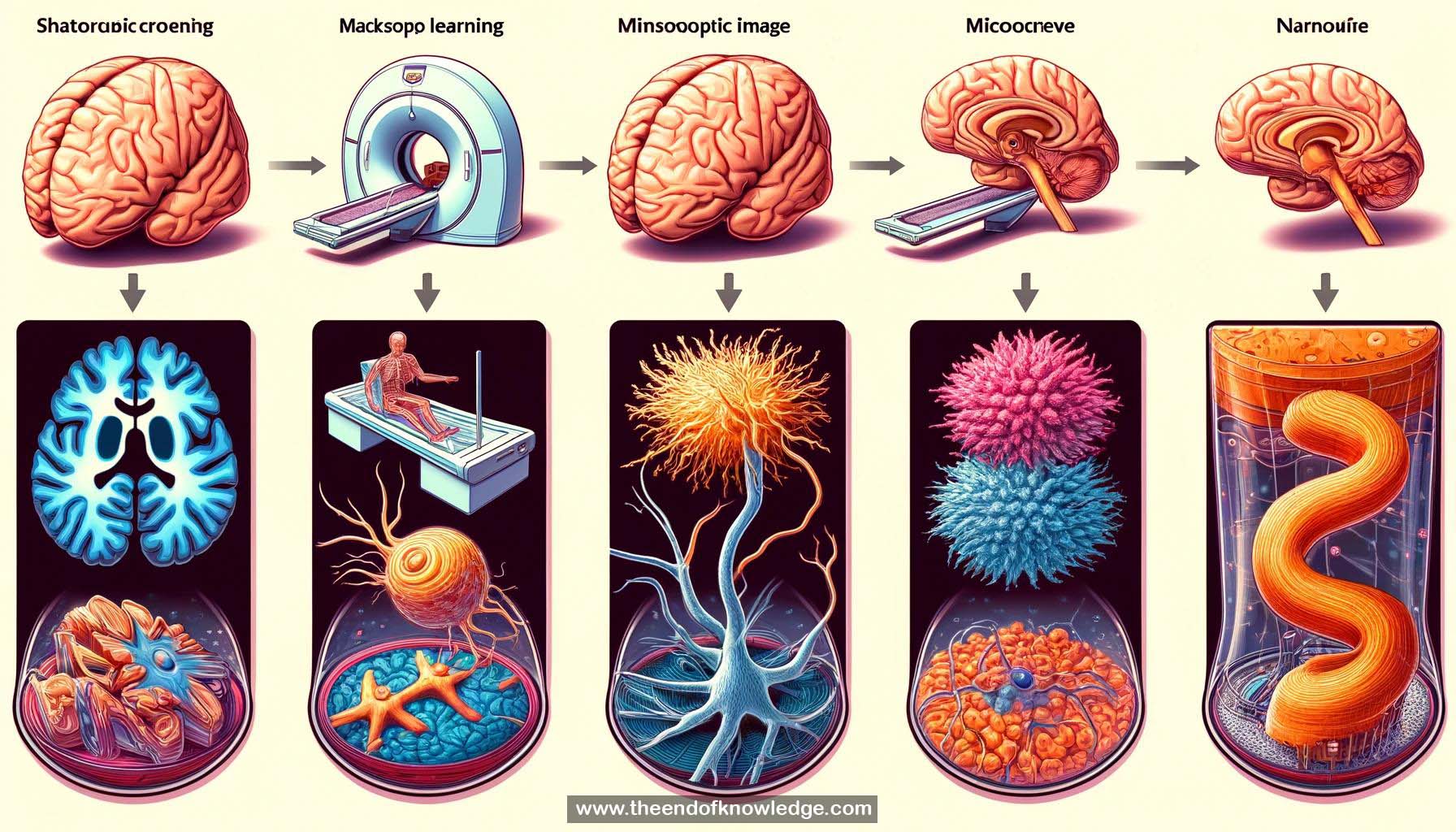
2.- Imágenes biomédicas: Estudio de estructuras biológicas a través de técnicas de imagen a varias escalas (de órganos a moléculas).

3.- Vínculo entre forma y biología: La forma de una estructura biológica está vinculada a su función y estado de salud/enfermedad.

4.- Técnicas de imagen: RMN, microscopía, crio-microscopía electrónica permiten observar formas biológicas a diferentes escalas.

5.- Preguntas biomédicas: La investigación busca responder preguntas sobre cambios de forma biológica, por ejemplo, atrofia cerebral en Alzheimer.

6.- Reconstrucción de formas: Extracción de formas de imágenes a través de algoritmos como segmentación antes del análisis.

7.- Modelado/representación de formas: Representación numérica de formas extraídas en una computadora para análisis.

8.- Variedades: Generalizaciones de espacios vectoriales que pueden ser curvadas. Muchas representaciones de formas dan lugar a variedades.

9.- Formas como variedades: Una forma en sí misma puede ser una variedad (por ejemplo, la superficie de un objeto).

10.- Espacios de formas como variedades: El espacio de todas las formas posibles de un cierto tipo forma una variedad.

11.- Espacios de transformaciones de formas como variedades: Conjuntos de movimientos o deformaciones de formas pueden ser modelados como variedades.

12.- Generalizando estadísticas a variedades: Las estadísticas tradicionales no se aplican en variedades. Las estadísticas deben ser generalizadas.

13.- Geometría de variedades como sesgo inductivo: Incorporar conocimiento de la geometría del espacio de formas puede mejorar los algoritmos de aprendizaje automático.

14.- Tipos de problemas de aprendizaje automático: Supervisado, no supervisado, aprendizaje por refuerzo, optimización - todos pueden ser generalizados a variedades.

15.- Bloques de construcción de aprendizaje en variedades: Puntos, vectores tangentes, geodésicas, distancias, mapa exponencial - usados para traducir ML a variedades.

16.- Conversión de espacio vectorial a variedades: Traducir bloques de construcción de ML permite convertir muchos algoritmos a variedades.

17.- Paquete Geomstats: Paquete de Python de código abierto que implementa cálculos en variedades para aprendizaje en variedades/geométrico.

18.- Aprendizaje en variedades de Riemann: El paquete soporta varios algoritmos en variedades de Riemann (metrizable).

19.- Variedades de posición/transformación: Ejemplo de variedad es SE(3) - el espacio de rotaciones y traslaciones 3D.

20.- Taxonomía numérica de variedades: Jerarquía/taxonomía de variedades de abstracto a concreto, implementada en geomstats.

21.- Visión general de ML adaptado a variedades: La investigación busca generalizar algoritmos de ML a través de diferentes variedades.

22.- Reducción de dimensión en variedades: Generalizando técnicas de reducción de dimensión lineal (PCA) y no lineal (autoencoders) a variedades.

23.- Vista geométrica de reducción de dimensión: Encontrar subespacios principales dentro de espacios lineales o variedades.

24.- Autoencoders variacionales (VAEs): Aprender subespacio latente no lineal del espacio de datos asumiendo modelo generativo.

25.- Generalizando VAEs a variedades: Adaptando componentes de VAE (modelo generativo, función de pérdida) a versiones de variedades.

26.- Componentes de Manifold VAE (mVAE): El mapa exponencial reemplaza la suma. La distancia geodésica reemplaza la euclidiana. Funciones de pérdida adaptadas.

27.- mVAE vs alternativas: mVAE más rápido que el método de reducción de dimensión en variedades basado en MCMC.

28.- mVAE explica la curvatura del espacio latente de VAE: La perspectiva de variedades muestra por qué los VAEs tienden a aprender espacios latentes más planos.

29.- Pipeline general de análisis de formas: Extracción de formas, modelado, cálculo en variedades, generación de ideas.

30.- Investigación en curso: Generalizar aún más ML a variedades, aplicando a datos de formas biomédicas.

Bóveda de Conocimiento construida porDavid Vivancos 2024